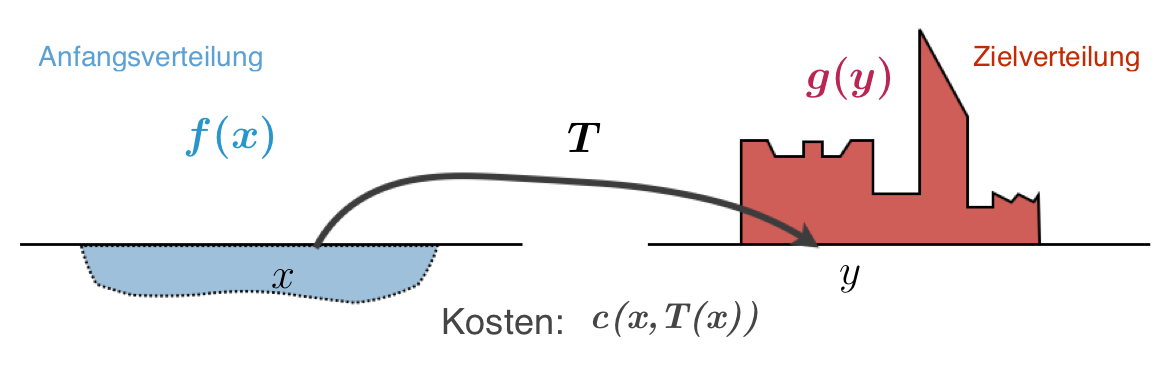
Das optimale Transportproblem beschäftigt sich mit der Frage, wie zwei gegebene räumliche Verteilungen von Masse (z.B. Sand) mittels einer Transportabbildung ineinander überführt werden können, so dass die Gesamtkosten des Transports minimal sind. Letztere sind durch eine Kostenfunktion gegeben, die die Transportkosten von einer „Einheit Masse“ zwischen zwei Punkten des Raums angibt. Ist die Kostenfunktion durch den Euklidischen Abstand im Raum gegeben, so führt das optimale Transportproblem auf die sogenannte Kantorovich-Wasserstein-Metrik, die zum Beispiel in statistischen Verfahren den „Abstand“ zwischen Bildern aus Magnetresonanztomographie-Verfahren angibt.
Seit dem Jahr 2000 konnte ferner ein wichtiger Zusammenhang zwischen der Theorie des optimalen Transports und partiellen Differentialgleichungen hergestellt werden, welcher Diffusionsprozesse z.B. durch poröse Medien beschreibt. Diese Prozesse laufen so ab, dass die Energie des Systems minimal wird. Dabei wird während einer Zustandsänderung Energie z.B. an die Umgebung abgegeben. Die dissipierte Energie dieser Änderung wird durch die Kantorovich-Wasserstein-Metrik gemessen. Die neue Interpretation dieser Gleichungen als metrische Gradientenflüsse führte zu einer neuen geometrischen Sichtweise auf die physikalischen Prozesse mit weitreichenden mathematischen Folgerungen.
Ein wesentlicher Nachteil dieses Konzeptes des optimalen Transportes ist, dass das Erzeugen und Vernichten von Masse nicht beschrieben werden kann. Insbesondere müssen die beiden Masseverteilungen die gleiche Gesamtmasse besitzen. In bildgebenden Verfahren wie der Magnetresonanztomographie lässt sich dieses Problem lösen, indem die beiden zu vergleichenden Bilder normalisiert werden. Dies löst jedoch nicht das Problem, dass im zweiten Bild neu entstandene Masse (z.B. karzinöses Gewebe) nicht beschreibbar ist, da sie nur das Ergebnis eines Transports sein kann.
Um dieses Problem zu lösen und die Theorie des optimalen Transports zu erweitern, werden am Weierstraß-Institut neue Abstandsbegriffe eingeführt, die eng verknüpft sind mit sogenannten Gradientenflüssen. Ein Gradientenfluss beschreibt die zeitliche Entwicklung eines Systems, die dem steilsten Abstieg einer Energie- oder Entropiefunktion folgt. Der Gradient dieses Funktionals ist gegeben durch eine Riemannsche Struktur, die den Mechanismus des Energie- oder Entropieverlusts beschreibt. Nahe des thermodynamischen Gleichgewichts lässt sich der Dissipationsmechanismus durch einen linearen, symmetrischen Operator ausdrücken, der als Onsager-Operator bezeichnet wird.
Mathematisch lässt sich der Onsager-Operator als das Inverse einer Riemannschen Metrik auffassen. Dadurch wird eine geometrische Struktur auf dem Raum der Maße eingeführt, die es insbesondere erlaubt, Abstände zwischen zwei Zuständen, die durch nicht-negative Maße gegeben sind, zu berechnen. Es ist nun aus mathematischer Sicht interessant, die geometrische Struktur, die aus dem physikalischen Prozess resultiert, näher zu charakterisieren. So sind zum Beispiel Fragen nach der Konvergenz bezüglich des neuen Abstands und die explizite Beschreibung kürzester verbindender Kurven (sogenannte Geodäten) relevant.
Dies gelang im Fall der sogenannten Hellinger-Kantorovich-Metrik, die mit der Gradientenflussformulierung einer skalaren Reaktions-Diffusionsgleichung verknüpft ist. Letztere beschreibt zum Beispiel das Entstehen und Verbreiten von biologischem Gewebe. Überraschenderweise kann die Hellinger-Kantorovich-Metrik wieder als ein Optimales-Transport-Problem auf einem erweiterten Raum mit komplizierteren Nebenbedingungen formuliert werden. Eine Besonderheit der Hellinger-Kantorovich-Metrik ist die Existenz eines scharfen Werts für den euklidischen Abstand der Masseverteilungen. Zwischen Punkten, deren euklidischer Abstand über diesem Wert liegt, ist ein Transport von Masse nicht mehr optimal – Masse muss hier erzeugt und vernichtet werden. Die Hellinger-Kantorovich-Metrik gehört zu einer Klasse verallgemeinerter Optimaler Transport-Probleme die als „Unbalanced transport“ oder Entropie-Transport-Probleme bezeichnet werden.