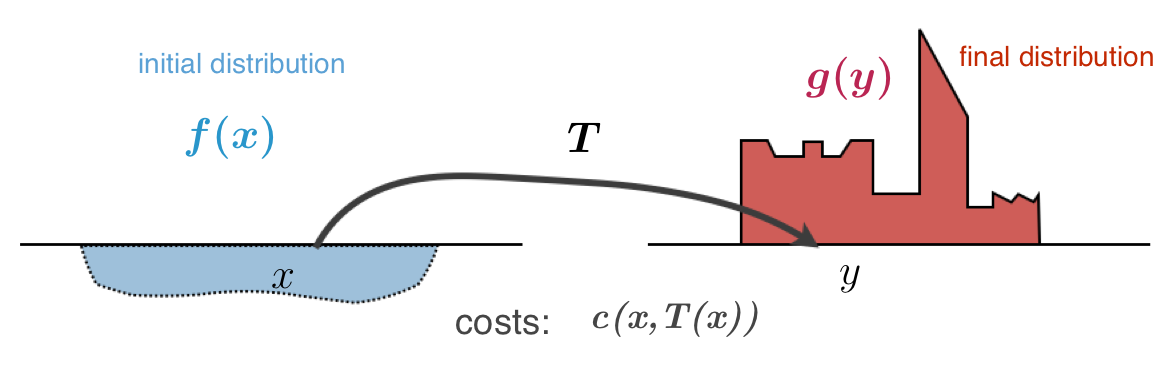
The optimal transport problem asks, essentially, how can we transport a mass of something (e.g. sand) from A to B with the least amount of effort or, more formally, how can we transform one spatial distribution of mass into another distribution by following a transport map that minimizes the total cost of that transformation. This involves using a cost function that determines the “cost of transporting a unit mass between two points in space”. If this cost function is stated in terms of Euclidean distance in space, then the optimal transport problem yields the so-called Kantorovich–Wasserstein metric, which provides the definition of “distance” as used in statistical methods such as comparing images from MRI scans.
Since the year 2000, an important correlation has furthermore been made between the theory of optimal transport and partial differential equations that describes diffusion processes, for example, through porous media. Such processes occur in a way that minimizes the energy of the system. Energy could be released to the environment, for example, during a change in state. The Kantorovich–Wasserstein metric is used to measure the energy dissipated through this change. Reinterpreting the equations as metric gradient flows reveals a new geometric perspective of the physical processes themselves, with far-reaching mathematical consequences.
A serious limitation to this treatment of optimal transport is that it cannot describe the creation and annihilation of mass. In particular, the two mass distributions A and B must always add up to the same total mass. An elegant solution does exist for imaging methods like magnetic resonance imaging, which evades the problem by normalizing the two images to be compared. However, it does not directly solve the problem, because it has no way of describing newly appearing mass in the second image (e.g. cancerous tissue) other than as the result of a transport.
To solve this problem, and to expand the theory of optimal transport itself, mathematicians at the Weierstraß Institute are introducing new terms of distance that are closely related to so-called gradient flows. A gradient flow describes the development over time of a system, following the steepest descent of an energy or entropy functional. The gradient of this functional is given by a Riemannian structure that describes the mechanism of energy or entropy loss. Near thermodynamic equilibrium, the dissipation mechanism can be expressed as a symmetric linear operator called the Onsager operator.
Mathematically, the Onsager operator can be understood as the inverse of a Riemannian metric. This introduces a geometric structure over the space of the measures, which, in particular, allows distances to be calculated between two states that are given by non-negative. It is now interesting from a mathematical perspective to characterize the cone structure that results from a physical process in greater detail. Relevant considerations include, for example, determining convergence with respect to the new distance and the explicit description of shortest connecting curves (so-called geodesics).
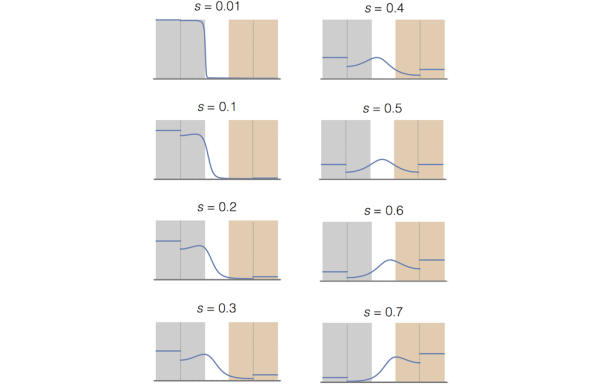
Such a characterization has been achieved for the so-called Hellinger–Kantorovich metric, in conjunction with a gradient flow formulation of a scalar reaction-diffusion equation. The latter describes the creation and spread of biological tissue, for example. Surprisingly, the Hellinger–Kantorovich metric can, in turn, be formulated as an optimal transport problem on an expanded space with complicated constraints. A special feature of the Hellinger–Kantorovich metric is the existence of a sharp value for the Euclidean distance of the mass distributions. Mass can no longer be optimally transported between points whose Euclidean distance lies beyond this value – mass must be created or annihilated at those distances. The Hellinger–Kantorovich metric belongs to a class of generalized optimal transport problems known as “unbalanced transport” or “entropy transport” problems.